Chaos Theory

Bear with us on the Chaos Theory article. It seems a bit technical upon first read, but it actually isn't as difficult to grasp as it may seem initially. Give it a go!

Traditional Newtonian physics is often understood as deterministic, where physical matter operates within fixed and knowable laws, there is cause and effect. Therefore, classically it has been assumed that it is theoretically possible that precise predictability of a system could be achieved if enough information about the system is collected and processed; if the momentum and velocity of every particle in the system was known to infinite precision. If there were small imprecisions in the initial conditions, the resulting description of the system was thought to be only slightly different from the prediction.

Chaos theory dramatically challenges this assumption, showing how systems that exhibit chaos will diverge exponentially with time from other very similar systems because of small differences in the initial data (chaos exhibits an extreme sensitivity to initial conditions), this divergence is fundamental and these unpredictable aspects are described as random (Crutchfield, Farmer, Packard and Shaw 46). There is no clear relationship between cause and effect; the scenario of Newtonian physics breaks down. Specifically chaos theory challenges the idea that “a system can be understood by breaking it down and studying each piece” (Crutchfield, Farmer, Packard and Shaw 56).

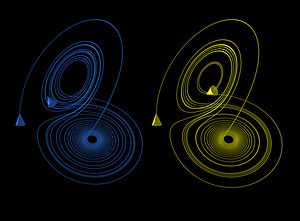
More generally, chaos theory deals with the behavior of deterministic, nonlinear, dynamical[1] systems that exhibit chaos (https://www.phy.duke.edu/research-activities-dan-gauthiers-group). However, the behavior of chaos, the result from these systems with fixed rules that have no elements of chance, a “simple nonlinear interaction of only a few components” (Crutchfield, Farmer, Packard and Shaw 56) actually has more complicated behavior than simply “random”. The surprising and complicated behavior of chaos and the reason there can be a chaos theory is that chaos produces an underlying order or pattern in its behavior, visually represented by strange attractors. We will see order or patterns in the chaos; however, the inherent randomness implies there are basic limits on our ability to make specific predictions about these types of systems. Think about that for a minute. Chaos has a theory?! There are underlying patterns in the behavior of chaos? We can't make specific predictions about chaos, but we can see the underlying order in it.

Edward Lorenz is a central figure in chaos theory. He was working on weather predictions in 1961, running simulations on a computer. He decided to run a sequence of data a second time through the simulation. In order to save time, he ran the simulation starting half way through. When he looked at the weather printout, the simulation had created a completely different weather calculation. Baffled, he examined the data and realized that he had entered a data set to only three significant digits, rather than the previous simulation, which had been calculated to five significant digits. The very small change, which Lorenz (and Newtonian-physics understanding at the time) had assumed would be basically inconsequential, produced dramatic differences in the long term weather outcome. The program Lorenz was using classical and used a purely deterministic system of equations. If there was a particular starting point the weather would unfold a certain way, with a slightly different point, there would be a slightly different weather pattern. “A small numerical error was like a small puff of wind-surely the small puffs faded or canceled each other out before they could change important, large-scale features of the weather” (www.gweep.net/-rocko). However using the equations in the program that Lorenz did, the small differences had extreme effects. “This occurrence led Lorenz to the conclusion that complex systems such as the weather are incredibly sensitive on the initial conditions of the system” (www.duke.edu/-mjd). Lorenz labeled this incredible dependence on the initial conditions the “Butterfly Effect” in a paper he wrote in 1979, Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set off a Tornado in Texas? Lorenz investigated this idea, sensitivity in initial conditions, further and created a simple system of three nonlinear differential equations in order to model the action of the chaotic behavior of a gaseous system.